



© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física

Cinemática

Capítulo 3.5 – Lançamento horizontal - balística
A
palavra
balística
tem
origem
no
grego
ballein,
que
significa
“lançar”.
Esse
ramo
da
física
estuda
o
lançamento,
o
comportamento
durante
o
voo
e
os
efeitos
do
impacto
de
projéteis.
Para
compreendê-lo,
é
fundamental
retomar-
mos
os
conceitos
da
Cinemática,
especialmente
os
movimentos
retilíneos
—
o
movimento
uniforme
e
o
uniformemente
variado
—
que
descrevem
o
desloca-
mento unidimensional de um corpo.
Agora,
ampliaremos
essa
análise
para
movimentos
em
duas
dimensões
,
aplicando
os
mesmos
princípios
da
cinemática.
O
exemplo
clássico
desse
tipo
de
movimento
é
o
de
um
projétil,
nome
dado
a
qualquer
corpo
lançado
no
es-
paço cuja única força atuante, após o lançamento, é a
gravidade.
O
primeiro
estudioso
a
aplicar
um
tratamento
matemático
ao
estudo
da
balística
foi
o
matemático
italiano
Niccolò
Fontana
Tartaglia
(1499–1557),
autor
do
livro
La
nuova
scientia.
Nessa
obra
pioneira,
Tartaglia
combinou
os
conheci-
mentos
de
matemática
com
a
prática
da
artilharia,
analisando
a
trajetória
dos
projéteis
e
investigando
qual
ângulo
de
lançamento
maximizaria
o
alcance
de
um disparo de canhão — como ilustrado na figura abaixo.
Mais
tarde,
em
sua
obra
Quesiti
et
inventioni
diverse
,
Tartaglia
retomou
as
questões
militares
e
propôs
uma
descrição
da
trajetória
de
um
projétil
dividi-
da em três fases:
Trajetórias
de
três
objetos
lançados
no
mesmo
ângulo
(70°).
Autor
Allen
McC.
Este
arquivo
está
licenciado
sob
a
licença Creative Commons


Na
figura,
Tartaglia
indica
a
posição
de
disparo
de
um
canhão
formando
um
ângulo
de 45º,
livro “Quesiti et inventioni diversas”
lustração
do
livro
“Quesiti
et
inventioni
diversas”,
mostrando
a
trajetória
do
projétil
3.5.a
Um pouco de história


A
figura
abaixo
ilustra
alguns
exemplos
de
projéteis.
Todo
corpo
que,
após
ser
lançado,
passa
a
se
mover
apenas
sob
a
ação
da
gravidade
é considerado um projétil. Isso inclui:
•
Um
corpo em queda livre
, com
velocidade inicial igual a zero
;
•
Um
corpo
lançado
verticalmente
para
cima
,
que
desacelera
até
parar
momentaneamente
no
ponto
mais
alto
e,
em
seguida,
retorna à Terra;
•
O
lançamento oblíquo
, em que o corpo é lançado formando um
ângulo com a horizontal,
descrevendo uma trajetória curva no ar;
•
E
o
caso
clássico
da
bala
de
canhão
disparada
horizontalmente
a
partir
de
uma
certa
altura,
que
percorre
uma
trajetória
parabólica
ao mesmo tempo em que cai.
Esses
são
todos
exemplos
de
movimento
bidimensional,
nos
quais
a
análise
pode
ser
feita
separando
os
movimentos
horizontal
(com
velocidade
constante)
e
vertical
(com
aceleração
devido
à
gravidade)
.
Essa
separação
é
a
chave
para
entender
o
comportamento
dos
projéteis
no ar.
•
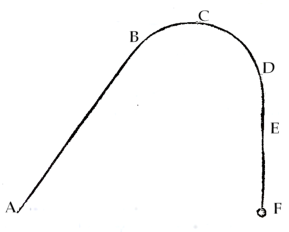
Um trecho reto, impulsionado pela força da pólvora (de A até B), chamado de moto violento;
•
Uma curva, resultado da ação da gravidade (de B até D), o moto natural;
•
E, por fim, uma linha reta vertical, na qual o projétil cai perpendicularmente ao solo (de D até F).
Apesar de seus avanços, Tartaglia não chegou a descrever com precisão a verdadeira trajetória parabólica de um projétil. Sua obra,
Nuova scientia, publicada em Veneza, em 1537, foi a primeira a abordar sistematicamente a teoria e a prática da artilharia. Ele identificou
corretamente que o ângulo de 45º proporcionava o alcance máximo, mas não conseguiu demonstrar matematicamente essa conclusão,
mantendo ainda concepções equivocadas da época sobre o movimento dos projéteis.
Mesmo assim, Tartaglia foi responsável por um marco importante: introduziu o tratamento científico no estudo da balística, lançando
as bases para os desenvolvimentos posteriores, inclusive os realizados por Galileu Galilei no século seguinte.
Homem bala - Foto gentilmente cedida por Ennor, Barry
Human Cannonball @ the Royal Cornwall Show 2007
Esses tipos de lançamentos estão presentes em diversas situações do cotidiano, especialmente em contextos históricos, esportivos e
militares.
Nas armas de arremesso, por exemplo, projéteis são usados para lançar pedras, lanças e flechas contra inimigos, predadores ou presas.
Em tempos mais modernos, esse princípio se aplica a armamentos como balas, granadas, projéteis de artilharia e outros dispositivos similares,
todos baseados nos fundamentos da balística.
Nos esportes, o movimento de projéteis também é amplamente observado:
•
Em jogos como beisebol, críquete, futebol e boliche, onde bolas são lançadas ou arremessadas;
•
Nas apresentações de malabarismo, com objetos sendo lançados e pegos em trajetórias bem definidas;
•
No atletismo, com modalidades como o lançamento de disco, martelo, peso e dardo, além do salto com vara e o salto em distância,
que envolvem trajetórias parabólicas no ar.
Desconsiderando os efeitos da resistência do ar, um projétil é qualquer corpo que, após ser lançado ou abandonado, passa a se mover
somente sob a ação da gravidade. Se houver qualquer outra força atuando sobre ele — como propulsão contínua ou controle aerodinâmico —
ele não será considerado um projétil no sentido físico. Um exemplo é o míssil de cruzeiro, que mantém voo motorizado e guiado por sistemas
eletrônicos, diferentemente de um projétil que segue apenas sob influência gravitacional após o lançamento.
É comum que os estudantes tenham dificuldade em aceitar que a única força atuando sobre um projétil em pleno voo (em um modelo
ideal, sem ar) é a gravidade — inclusive quando o corpo está subindo. Nesse caso, o projétil desacelera enquanto sobe, até atingir a altura
máxima, onde sua velocidade vertical é nula. A partir daí, ele inicia o movimento descendente, acelerando novamente em direção ao solo. Esse
comportamento já foi estudado nos movimentos verticais e agora se integra ao estudo dos lançamentos oblíquos e horizontais.


lançamento de disco
lançamento do martelo
lançamento do dardo

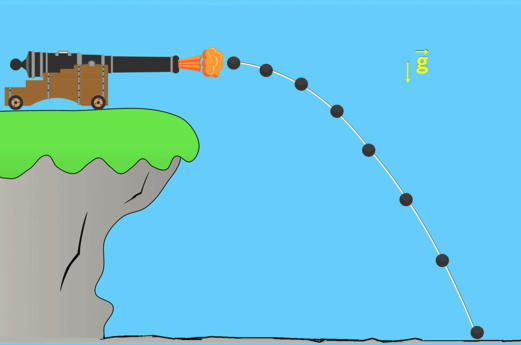
Agora,
vamos
imaginar
uma
situação
hipotética:
suponha
que
exista
um
“interruptor
da
gravidade”
e
que,
inicialmente,
ele
esteja
ligado.
Uma
bala de canhão
é disparada
horizontalmente
do topo de um penhasco.
A pergunta que surge é:
Que efeito a gravidade terá sobre o movimento da bala de canhão?
Mais especificamente:
1
.
A gravidade afeta o movimento horizontal
da bala de canhão?
2
.
A bala de canhão percorrerá uma
distância horizontal maior ou menor
devido à influência da gravidade?
A resposta para ambas as perguntas é: Não!
A
gravidade
não
interfere
no
movimento
horizontal
do
projétil.
Ela
atua
exclusivamente
na
direção
vertical,
puxando
a
bala
de
canhão
para
baixo.
O
movimento
horizontal
ocorre
com
velocidade
constante,
enquanto
o
movimento
vertical
é
uniformemente
acelerado,
com
aceleração igual à da gravidade (g ≈ 9,8 m/s²).
Portanto:
•
A distância horizontal
que a bala percorre
não depende da gravidade
, mas sim da
velocidade inicial horizontal
e do
tempo de queda.
•
O
papel
da
gravidade
é
f
azer
com
que
a
bala
caia
,
ou
seja,
encurtar
o
tempo
que
ela
permanece
no
ar
,
o
que
pode
limitar
a
distância
horizontal total percorrida.
•
Mas ela
não desacelera nem acelera
o movimento horizontal.
Se,
por
outro
lado,
o
“
interruptor
da
gravidade”
estivesse
desligado,
a
bala
seguiria
em
linha
reta
horizontalmente
para
sempre
(ou
até
encontrar um obstáculo), com velocidade constante, já que nenhuma força agiria sobre ela.
Esse
exemplo
ajuda
a
ilustrar
uma
das
ideias
mais
importantes
da
física:
os
movimentos
horizontal
e
vertical
são
independentes
e
devem ser analisados separadamente em um lançamento.

A
gravidade
atua
verticalmente
sobre
a
bala
de
canhão,
afetando
especificamente
seu
movimento
vertical.
Ela
é
a
responsável
por
produzir
uma
aceleração
constante
para
baixo
,
fazendo
com
que
a
bala
se
desvie
de
sua
trajetória
retilínea
original
e
inicie
uma
queda
vertical
em relação à linha reta que seguiria caso não houvesse gravidade.
Essa
força
—
exercida
pela
Terra
sobre
qualquer
corpo
com
massa
—
é
o
que
determina
o
movimento
para
baixo
do
projétil,
originando
a
trajetória curva característica,
que chamamos de
trajetória parabólica.
Nesse contexto, o movimento do projétil resulta da c
omposição de dois movimentos simultâneos e independentes:
•
No
eixo
horizontal
(eixo
X),
o
projétil
segue
com
velocidade
constante
,
já
que
nenhuma
força
atua
nessa
direção
(lembrando
que
estamos
desconsiderando a resistência do ar
).
•
No
eixo
vertical
(eixo
Y)
,
o
projétil
realiza
um
movimento
uniformemente
variado
(MUV),
ou
seja,
um
movimento
acelerado
com
aceleração constante,
chamada de
aceleração da gravidade
(g ≈ 9,8 m/s²).
Uma
das
ideias
mais
importantes
ilustradas
por
esse
tipo
de
movimento
é
a
de
que
os
movimentos
horizontal
e
vertical
são
independentes.
Essa
compreensão
foi
formulada
pela
primeira
vez
por
Galileu
Galilei,
que
reconheceu
que
a
gravidade
só
afeta
o
componente
vertical do movimento. Ele utilizou esse princípio para
prever o alcance de um projétil,
lançando as bases do estudo moderno da balística.
Esse
princípio
da
independência
dos
movimentos
é
essencial
para
a
análise
de
lançamentos
oblíquos
e
horizontais,
pois
permite
que
cada componente do movimento seja estudado separadamente, com suas próprias características e equações.
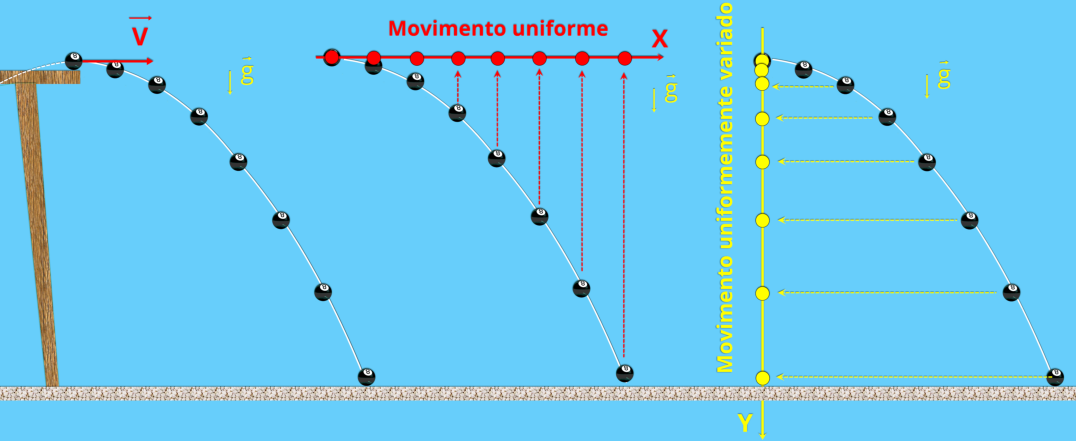

Neste
tópico,
você
aprenderá
como
as
componentes
horizontal
(x)
e
vertical
(y)
da
velocidade
e
do
desloca-mento
de
um
projétil
evoluem
com
o
tempo
—
algumas
permanecem
constantes,
enquanto
outras variam de forma previsível.
Vamos
retomar
o
exemplo
da
bala
de
canhão
lançada
horizontalmente
do
topo
de
um
penhasco.
Suponha
que
ela
seja
disparada
sem
ângulo
de
elevação
,
com
uma
velocidade
inicial
de
20
m/s
apenas
na
direção horizontal.
Se
não
existisse
a
gravidade,
a
bala
continuaria
indefini-damente
seu
movimento
horizontal
a
20
m/s,
em
linha
reta.
No
entanto,
devido
à
presença
da
gravidade,
a
bala
passa
a
a
celerar
para
baixo
com
uma
aceleração
cons-tante
de
aproximadamente
10
m/s²
(adotando o valor aproximado para facilitar os cálculos).
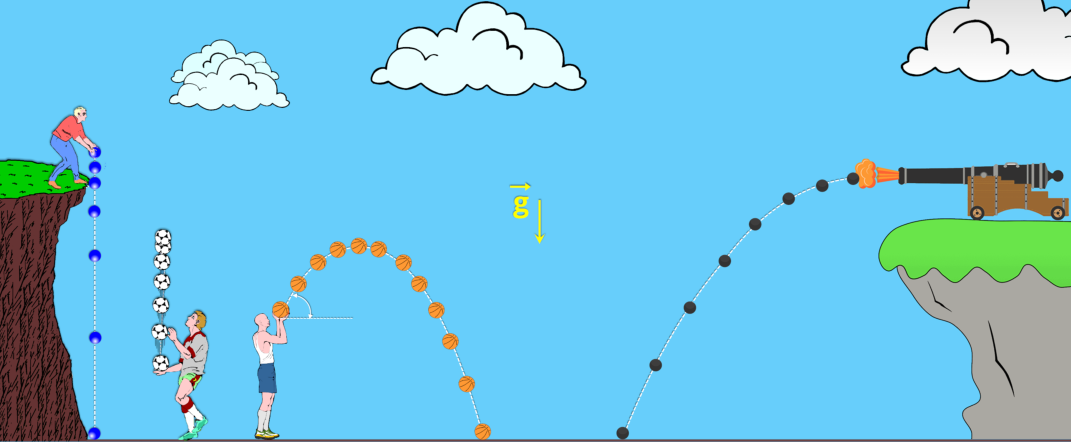
Isso
significa
que
a
velocidade
vertical
(Vy)
aumenta em
10 m/s a cada segundo:
http://www.ciencia-cultura.com/
https://www.ciencia-cultura.com/
https://www.ciencia-cultura.com/
http://www.ciencia-cultura.com/
http://www.ciencia-cultura.com/
http://www.ciencia-cultura.com/
A
Figura
compara
uma
bala
de
canhão
em
queda
livre
(em
azul)
a
uma
bala
de
canhão
lançada
horizontalmente
em
movimento
de
projétil
(em
vermelho). Você pode ver que a bala de canhão em queda livre cai na mesma proporção que a bala de canhão em movimento de projétil.
A
trajetória
curva
de
objetos
em
movimento
de
projétil
foi
mostrada
por
Galileu
como
uma
parábola,
mas
também
pode
ser
uma
linha
reta
no
caso
especial quando é lançada diretamente para cima ou para baixo.
Neste
vídeo
você
verá
algu-
mas
situações
no
lança-
mento
horizontal,
onde
a
velocidade
aumenta
e
con-
sequentemente
aumenta
o
alcance.
3.5.c
Exercícios resolvidos
R1.
Uma bola de bilhar rola sobre uma mesa com velocidade constante de 4 m/s. Após sair da mesa, cai, atingindo o chão a uma distância de
2 m dos pés da mesa. Desprezando os efeitos do ar, determine, aproximadamente, a altura da mesa. Adote g = 10m/s
2
.
Resolução:
Dicas para resolver exercícios sobre lançamento horizontal de projéteis.
Por conta do grande número de dados fornecidos no enunciado da questão, precisamos ser organizados. Vamos ser objetivos e práticos
na resolução dos exercícios. A seguir, estão algumas etapas importantes que facilitam muito a análise e a solução de problemas envolvendo
lançamento horizontal:
1.
Organize os dados fornecidos, separando claramente as informações relacionadas aos dois eixos:
o
Eixo X (horizontal): geralmente envolve velocidade constante.
o
Eixo Y (vertical): envolve queda livre, com aceleração da gravidade.
2.
Desenhe um esquema da situação descrita. Representar o cenário graficamente ajuda a visualizar a trajetória, identificar os vetores e
aplicar as equações corretas.
3.
Escolha as equações adequadas para cada eixo:
4.
No eixo X:
a.
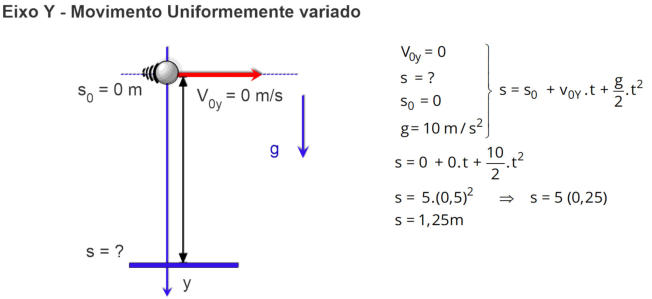
No eixo Y: (deslocamento vertical em função do tempo)
5.
O tempo (t) é a variável que conecta os dois eixos, pois é o mesmo para o movimento horizontal e vertical. Portanto, ele é a chave
para interligar as equações dos dois sentidos do movimento.
6.
Decida por onde começar: em muitos casos, é mais fácil encontrar o tempo usando os dados do eixo Y (altura, por exemplo), e só
depois aplicá-lo no eixo X para calcular o alcance ou a posição horizontal.
Essas etapas são fundamentais para resolver corretamente os problemas. A clareza na separação dos dados e o uso estratégico do
tempo tornam a análise mais simples e precisa.
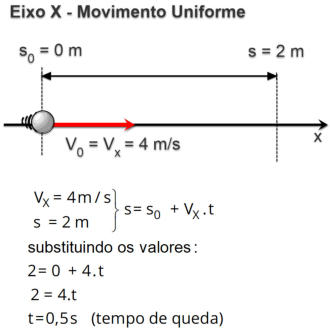
Eixo X
Eixo Y
V
0
= V
X
= 4 m/s
S
0Y
= 0 m
S
X
= 2 m
V
0Y
= 0 m/s
S
0
= 0 m
g = 10 m/s
2
t
queda
= ?
S
Y
= ?
t
queda
= ?
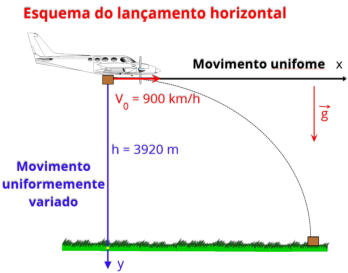
R2.
(FEI
-
SP)
Um
bombardeiro
voa
a
3920
m
de
altura
com
velocidade
de
900
km/h.
De
que
posição
ele
deve
soltar
uma
bomba
para
atingir
um
alvo no solo? Adote g = 10 m/s
2
.
Resolução:

3.5.d
Exercícios
propostos
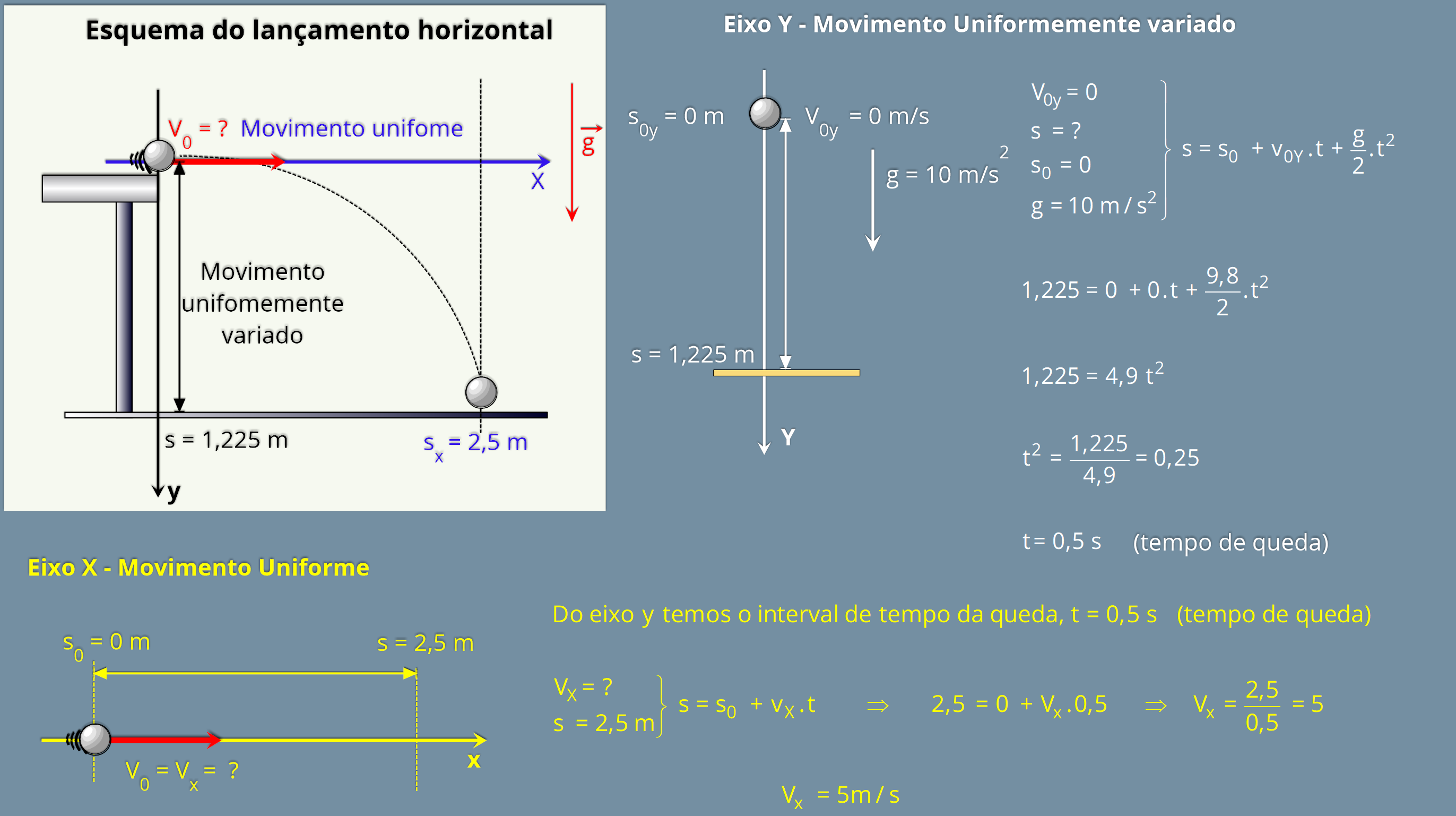
P1.
(UFPR)
Uma
bola
rola
sobre
uma
mesa
horizontal
de
1,
225
m
de
altura
e
vai
cair
num
ponto
do
solo
situado
à
distância
de
2,5
m,
medida
horizontalmente a partir da beirada da mesa. Qual a velocidade da bola, em m/s, no instante em que ela abandonou a mesa?
Adote g = 9,8 m/s
2
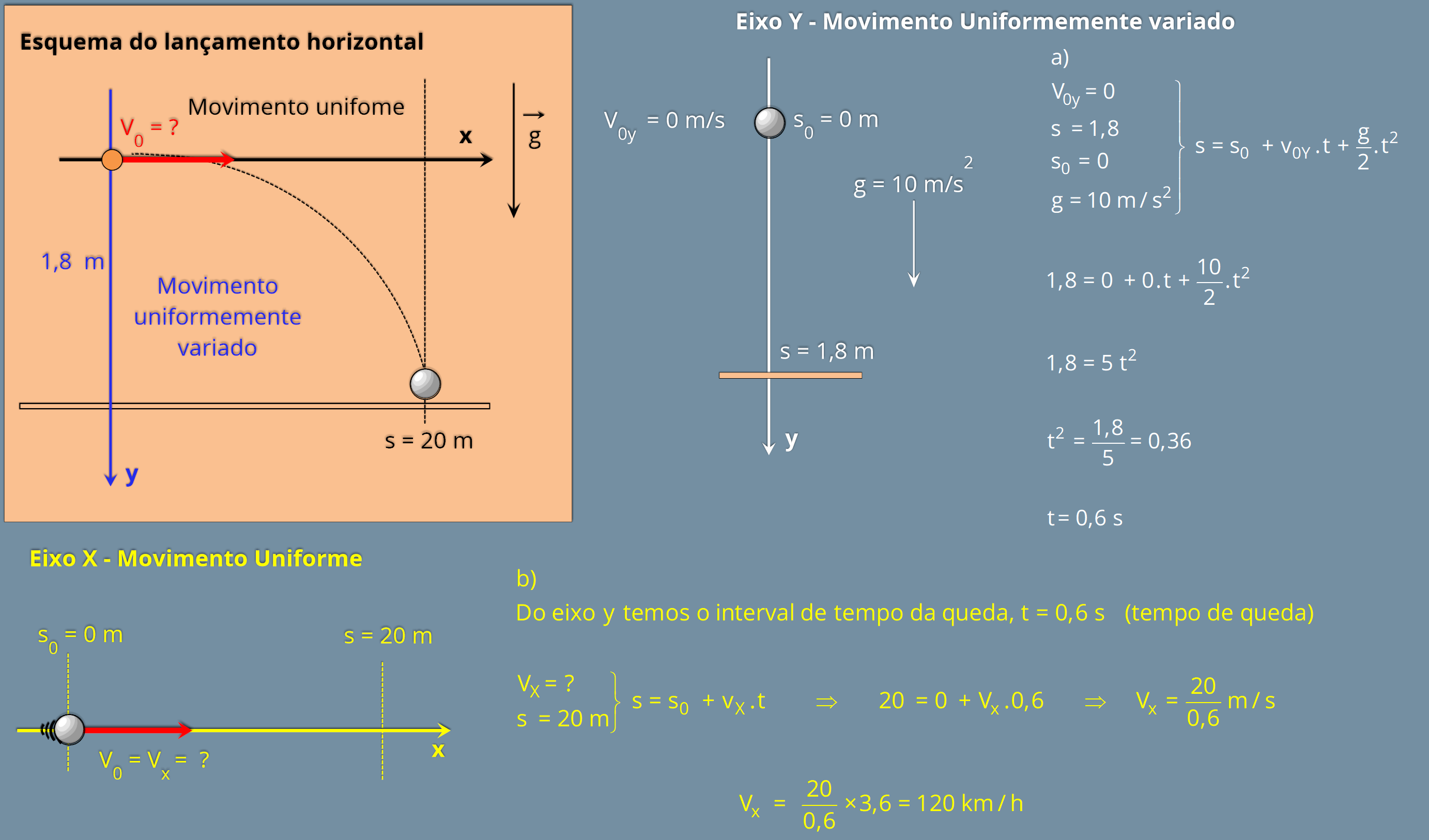
P2
(Unicamp-SP)
De
um
ponto
PM,
a
uma
altura
de
1,8
m,
lançou-se
horizontalmente
uma
bomba
de
gás
lacrimogêneo
que
atingiu
os
pés
de
um professor universitário a 20 m de distância, como indica a figura. (Dado: g = 10 m/s
2
).
a) Quanto tempo levou a bomba para atingir o professor?
b) Com que velocidade v
o
(em km/h) foi lançada a bomba?
P3.
(CEFET
-
PR)
Um
menino
posicionado
na
borda
de
uma
piscina
atira
uma
pedra
horizontalmente
da
altura
de
1m
da
superfície
da
água.
A
pedra atinge a água a
3 m da borda. Determine a velocidade, em m/s, com que o menino a lançou, considerando g= 10m/s
2
e desprezando a resistência do ar.
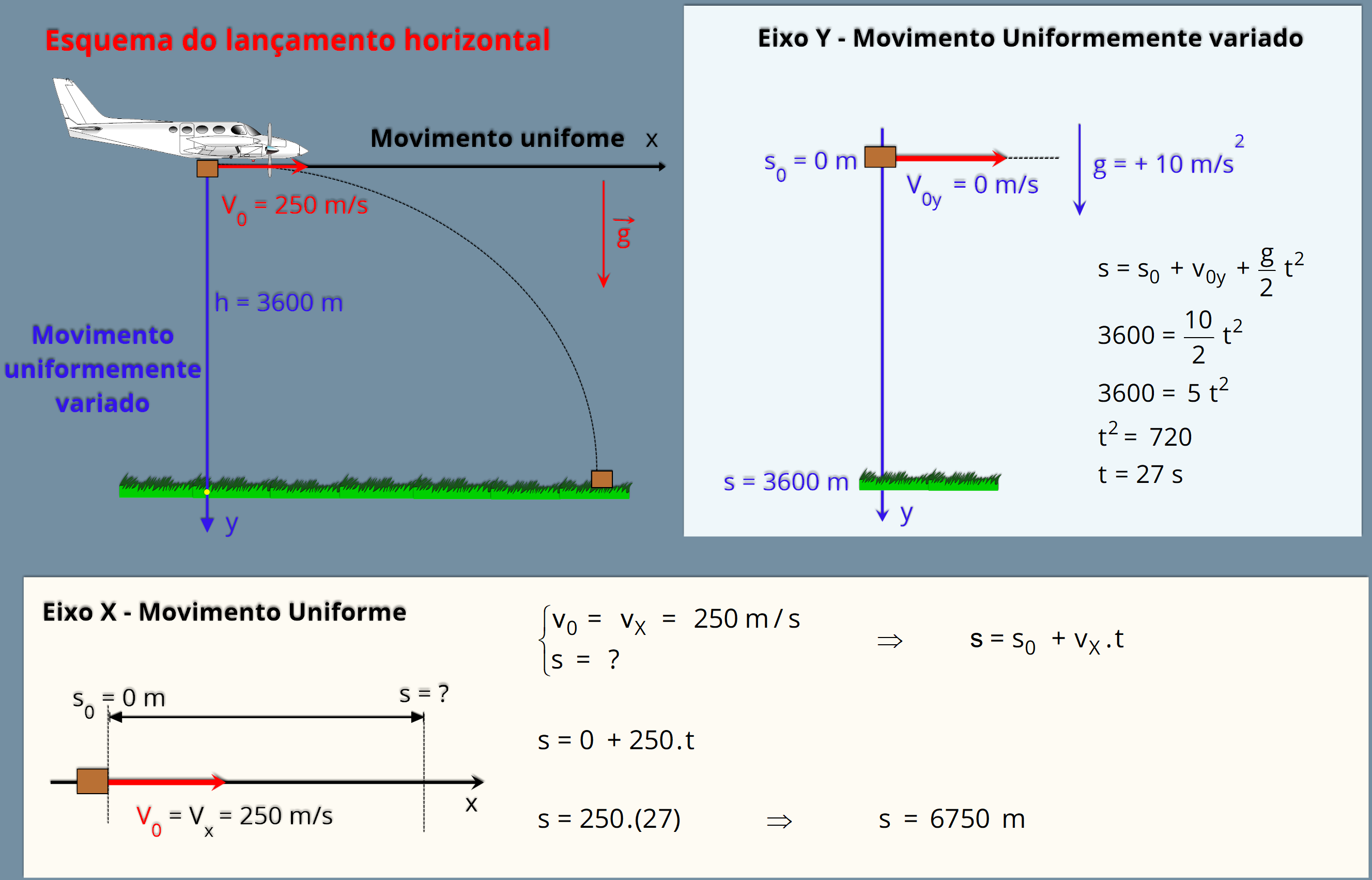
P4.
Um
avião
de
salvamento,
sobrevoa
uma
região
a
uma
altura
de
3600
m
do
solo
e
com
velocidade
de
250
m/s,
deve
deixar
cair
um
pacote
para
um
grupo
de
pessoas
que
ficaram
isoladas
após
um
acidente.
Para
que
o
pacote
atinja
o
grupo,
deve
ser
abandonado
t
segundos
antes
de
o avião passar diretamente acima do grupo.
Adotando g = 10 m/s
2
e desprezando a resistência oferecida pelo ar, determine:
a) o valor de t;
b) a que distância da vertical, em que o pacote foi lançado, ele atinge o solo;
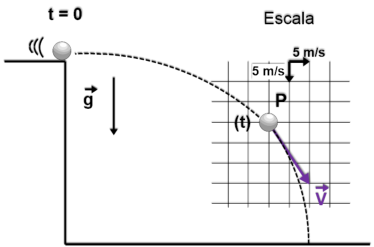
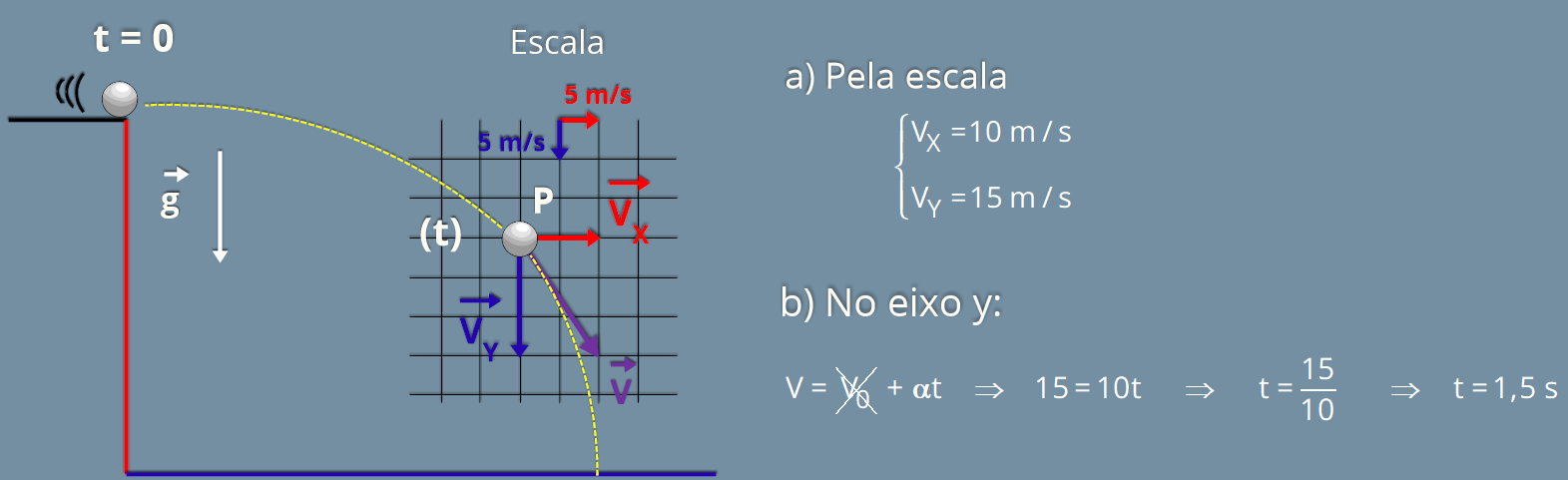
P5.
(UNESP
93)
Uma
pequena
esfera
é
lançada
horizontalmente
do
alto
de
um
edifício
com
velocidade
.
A
figura
a
seguir
mostra
a
velocidade
da
esfera
no
ponto
P
da
trajetória,
t
segundos
após
o
lançamento,
e
a
escala
utilizada
para
representar
esse
vetor
(as
linhas
verticais
do
quadriculado
são
paralelas
à
direção do vetor aceleração da gravidade).
Considerando
g
=
10
m/s
2
e
desprezando
a
resistência
oferecida
pelo
ar,
determine, a partir da figura:
a) o módulo de ;
b) o instante t em que a esfera passa pelo ponto P.
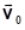
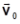
P6.
(UNESP
89)
Em
voo
horizontal,
a
3000
m
de
altitude,
com
velocidade
de
540
km/h,
um
bombardeiro
deixa
cair
uma
bomba.
Esta
explode
15
s
antes de atingir o solo. Desprezando a resistência do ar, calcule a velocidade da bomba no momento da explosão. Adote g = 10m/s
2
.
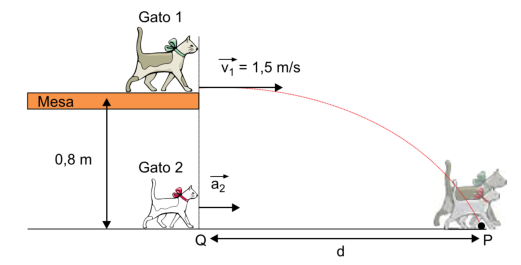
P7.
(Famerp
2022)
Dois
gatos
estão
brincando
num
local
onde
g
=
10
m/s
2
conforme
representado
na
imagem.
O
gato
1
se
encontra
sobre
o
tampo
de
uma
mesa,
a
0,8
m
do
chão.
O
gato
2,
que
está
no
chão,
na
mesma
vertical
Q
que
passa
pelo
gato
1,
inicia
uma
corrida,
a
partir
do
repouso,
com
aceleração
a
2
constante.
No
mesmo
instante,
o
gato
1
salta
horizontalmente
para
frente,
com
velocidade
horizontal
V
1
=
1,
5
m/s
levando
0,40
s
para
atingir
o
chão.
Por
fim,
os
dois
gatos
chegam
ao
ponto
P
no
mesmo
instante.
Para
a
resolução
da
questão,
despreze
as
dimensões dos gatos.
a)
Após
saltar,
qual
era
o
módulo
da
aceleração
do
gato
1,
em
m/s
2
.
Qual
era
o
módulo
da
componente
vertical
de
sua
velocidade,
em
m/s,
quando atingiu o chão?
b)
Quanto
vale
a
distância
d,
em
metros,
entre
a
linha
vertical
Q,
de
onde
os
dois
gatos
partiram,
e
o
ponto
P,
onde
se
encontraram?
Qual
era
a
aceleração do gato 2, em m/s
2
para que ambos chegassem a esse ponto P no mesmo instante?
3.5.b Lançamento horizontal
•
Após 1 segundo, Vy = 10 m/s;
•
Após 2 segundos, Vy = 20 m/s;
•
E assim por diante.
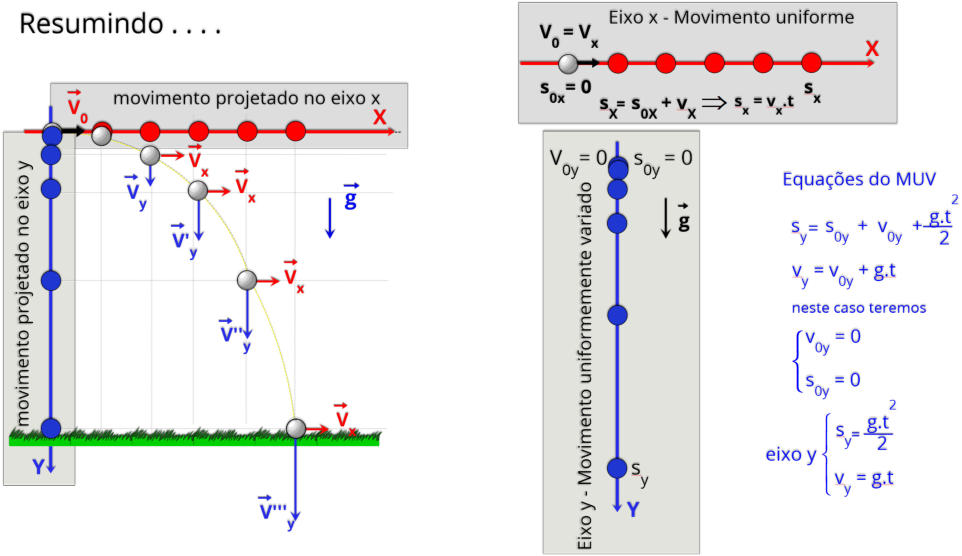
Se representarmos esse movimento em um
diagrama de vetores de velocidade
, veremos claramente o que acontece com cada
componente:
•
O
vetor da velocidade horizontal (Vx)
mantém sempre o mesmo valor (20 m/s), com
módulo, direção e sentido constantes.
•
Já
o
vetor
da
velocidade
vertical
(Vy)
aumenta
seu
módulo
com
o
tempo,
sempre
apontando
para
baixo,
refletindo
a
ação
contínua
da
aceleração gravitacional.
Esse
diagrama
permite
visualizar
a
composição
vetorial
da
velocidade
total
da
bala
de
canhão
ao
longo
do
tempo.
A
combinação
das
duas componentes (Vx e Vy) forma um vetor resultante cuja direção se inclina progressivamente para baixo à medida que o tempo passa.
O conceito-chave ilustrado nesse exemplo é que:
•
O
movimento horizontal é uniforme
(velocidade constante);
•
O
movimento vertical é uniformemente acelerado
(velocidade varia com o tempo).
Essa
distinção
é
fundamental
para
entender
o
comportamento
de
projéteis
e
será
útil
na
resolução
de
problemas
envolvendo
lançamentos.
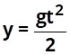
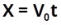
2.
Desenhe
um
esquema
da
situação
descrita
.
Representar
o
cenário graficamente ajuda a visualizar a trajetória.
3. Escolha as equações adequadas para cada eixo.
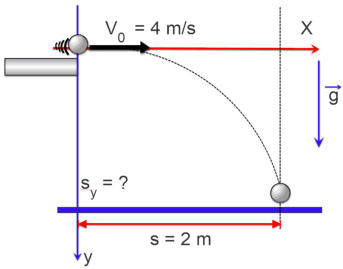
1.
Organize
os
dados
fornecidos
,
se-parando
claramente
as
informações
relacionadas
aos
dois eixos:
O tempo (t) é a variável que conecta os dois eixos, pois é o mesmo para o movimento horizontal e
vertical. Portanto, ele é a chave para interligar as equações dos dois sentidos do movimento.
http://www.ciencia-cultura.com/
2.
Desenhe
um
esquema
da
situação
descrita
.
Representar
o
cenário graficamente ajuda a visualizar a trajetória.
1.
Organize
os
dados
fornecidos
,
se-parando
claramente
as
informações
relacionadas
aos
dois eixos:
3. Escolha as equações adequadas para cada eixo.
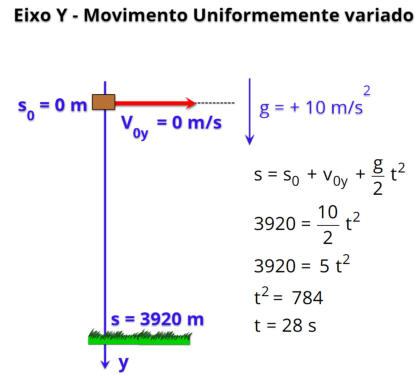
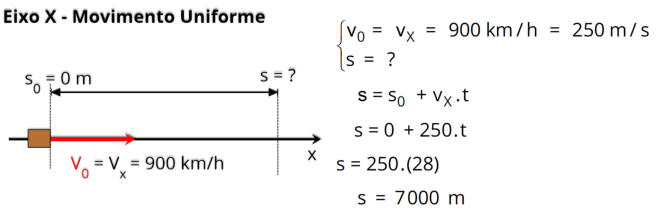

O tempo (t) é a variável que conecta os dois eixos, pois é o
mesmo para o movimento horizontal e vertical. Portanto,
ele é a chave para interligar as equações dos dois
sentidos do movimento.



https://www.flickr.com/photos/ennor/538533983
https://en.wikipedia.org/wiki/Ballistics
https://openstax.org/books/college-physics-2e/pages/3-4-projectile-motion










